I decided a great way to start 2022 was to solve this year's first Riddler! This is an optimization problem, where we solve for the strategy that minimizes the travel distance between three points along the edges of a triangle.

Amare the ant is traveling within Triangle ABC, as shown below. Angle A measures 15 degrees, and sides AB and AC both have length 1.
Amare starts at point B and wants to ultimately arrive on side AC. However, the queen of his colony has asked him to make several stops along the way. Specifically, his path must:

Start at point B.

Second, touch a point — any point — on side AC.

Third, touch a point — any point — back on side AB.

Finally, proceed to a point — any point — on side AC (not necessarily the same point he touched earlier).

What is the shortest distance Amare can travel to complete the queen’s desired path?

Setup

Let's create our own triangle diagram and use it to make some observations about a potential solution.

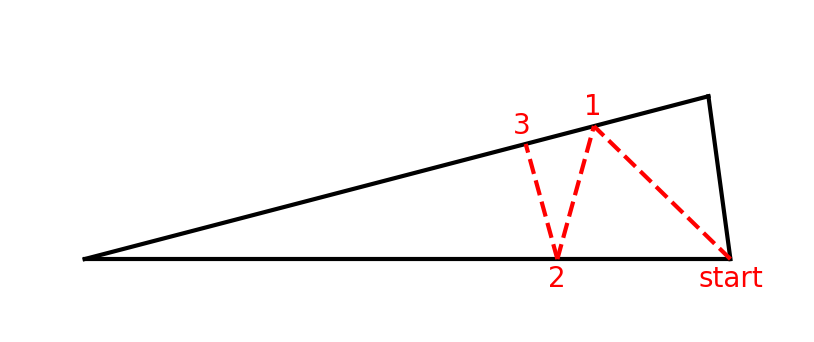
The first observation we can make is that there appears to be a tradeoff between the ant moving directly toward the top line right away, or moving to the left as he goes, in an effort to shorten the distance of the remaining segments. As the number of alternating stops tends toward infinity, the ant will be incentivized to move left early in his journey, which will make the first segment longer, but will shorten all future line segments.

Ultimately, we'd like to use some sort of optimization algorithm to solve for the ideal points, 1, 2, and 3. To do that, we need to write formulas for the total distance traveled as a function of the points we choose. While it's possible that people much smarter than me - puzzle solver Laurent Lessard, for example - could solve this analytically, I'll let the computer do (most of) the work for me.

The Math

We'll need a few functions to calculate the distance between points on our lines. The first function tells us the difference between a point, $a$ , along the baseline of the triangle, and a point, $b$ , along the top line, given that those lines intersect at an angle, $\theta$ . In this equation, $a$ and $b$ are single numbers that represent the distance from the lines' intersection to each point.

distance(a, b, \theta) = \sqrt{(a - b\times\cos(\theta)) ^ 2 + (b\times\sin(\theta)) ^ 2}

For example, the distance between the start point, $a = 1$ , and the end point of the top line, $b = 1$ , with an angle, $\theta = 15°$ , gives us $\approx{0.26105}$ . We can write this in Python as follows:

import math

def distance(a: float, b: float, theta: float) -> float:
    """
    Return the distance between two points on intersecting lines.

    We assume two lines intersect with angle theta at a point. Measuring from
    that point outwards, we choose points along each line a given distance away
    from the intersection, then return the distance between those points.

    Parameters
    ----------
    a : float, the distance from the intersection to a point on the first line.
    b : float, the distance from the intersection to a point on the second line.
    theta : float, the angle of intersection of the two lines, in degrees.

    Examples
    --------
    >>> # for a right triangle, the distance is equal to the hypotenuse
    >>> distance(3.0, 4.0, 90.0)
    5.0

    >>> # 180 degrees assumes points are in opposite directions
    >>> distance(3.0, 3.0, 180)
    6.0
    """
    rads = math.radians(theta)   # convert degrees into radians
    dx = b * math.cos(rads) - a  # distance between x-values of the points
    dy = b * math.sin(rads)      # distance between y-values of the points
    return (dx ** 2 + dy ** 2) ** 0.5

Then to calculate the total distance of all line segments, we can write a new function where we pass the points as a tuple, along with an angle, $\theta$ , and sum the distances between all pairs of points. In python, this can be implemented with a single list comprehension as follows.

from typing import Tuple

def total_distance(points: Tuple[float, ...], theta: float = 15) -> float:
    """Return the total distance of alternating points between two lines."""
    # calculate the distances between consecutive points, and sum all segments
    # add a 1.0 to the start of the points tuple because that's where we start
    points = (1.0,) + tuple(points)
    return sum(distance(a, b, theta) for a, b in zip(points, points[1:]))

Solution

Using an optimization engine, we find that the ant needs to travel a distance of ≈0.7071 by selecting the set of points (0.8165, 0.7321, 0.7071).

It turns out that the setup to the problem was 99% of the work. Rather than trudging through formulas and calculus, we can use the powerful scipy.optimize.minimize solver to do the heavy lifting. We pass our total_distance function to the optimization engine, along with a set of initial guesses. The engine then calculates the derivative of our function with respect to all input values, and solves for the points at which all partial derivatives are zero.

from scipy.optimize import minimize

result = minimize(total_distance, x0=(1.0, 1.0, 1.0), args=15)
#       fun: 0.7071067811865541
#  hess_inv: array([[0.3980166 , 0.35710939, 0.34512563],
#        [0.35710939, 0.55406504, 0.53529042],
#        [0.34512563, 0.53529042, 0.70655101]])
#       jac: array([ 7.45058060e-08, -4.47034836e-08, -1.49011612e-08])
#   message: 'Optimization terminated successfully.'
#      nfev: 40
#       nit: 7
#      njev: 10
#    status: 0
#   success: True
#         x: array([0.81649653, 0.73205072, 0.70710669])

Extending the Problem

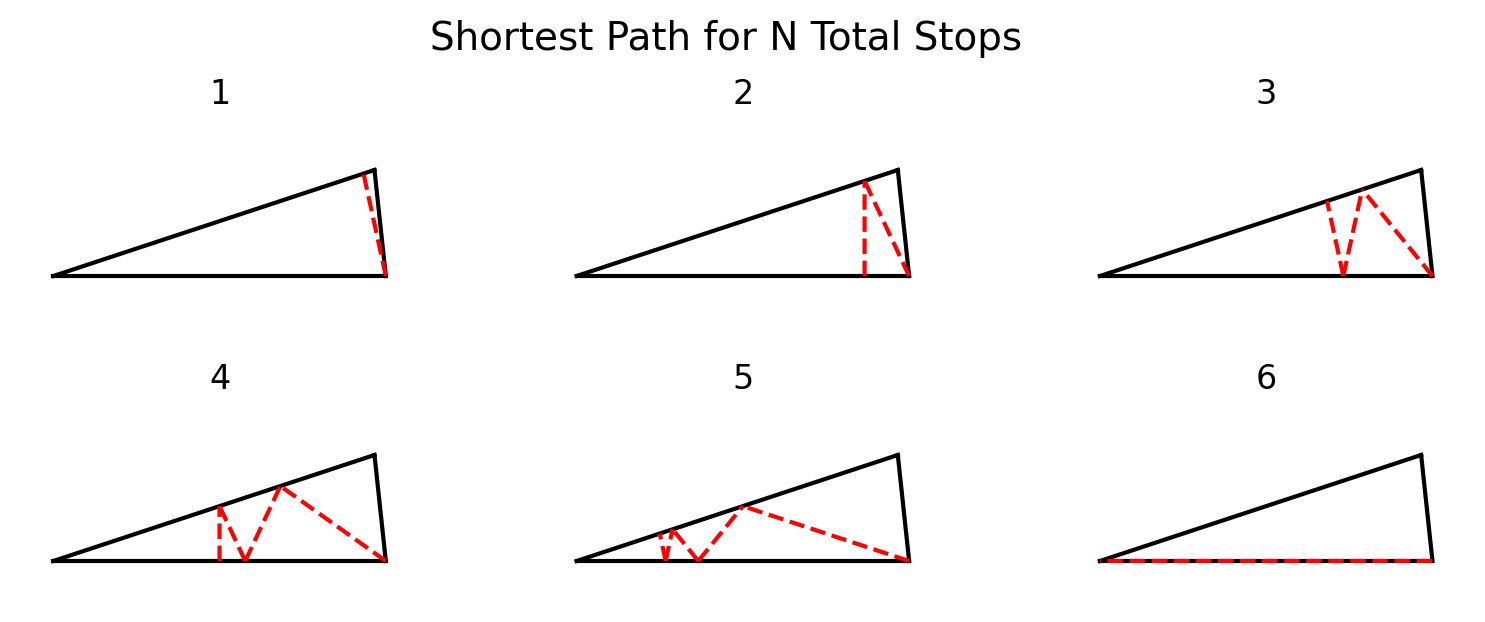
An interesting extension of the problem is to solve for the points Amare would select if he had to make 4 stops, or 5, or 6... At some point, as the number of stops increases, Amare should walk directly to the lines' intersection, then trivially bounce between them to complete his scavenging mission. The table below shows the distance he needs to walk for a given number of stops until that happens. We can see that once the Queen asks for 6 or more stops, Amare should walk directly to the intersection of the lines. Finally, we can also visualize the paths Amare would take, and we can see the first line heads further and further to the left as the number of stops increases.

Number of stops	Total Distance
1	0.25882
2	0.5
3	0.70711
4	0.86603
5	0.96593
6	1.0

Full Code

"""
Solving the Riddler Classic from Jan 7, 2022.
https://fivethirtyeight.com/features/can-you-trek-the-triangle/
"""
import math
from typing import Tuple
from scipy.optimize import minimize


def distance(a: float, b: float, theta: float) -> float:
    """
    Return the distance between two points on intersecting lines.

    We assume two lines intersect with angle theta at a point. Measuring from
    that point outwards, we choose points along each line a given distance away
    from the intersection, then return the distance between those points.

    Parameters
    ----------
    a : float, the distance from the intersection to a point on the first line.
    b : float, the distance from the intersection to a point on the second line.
    theta : float, the angle of intersection of the two lines, in degrees.

    Examples
    --------
    >>> # for a right triangle, the distance is equal to the hypotenuse
    >>> distance(3.0, 4.0, 90.0)
    5.0

    >>> # 180 degrees assumes points are in opposite directions
    >>> distance(3.0, 3.0, 180)
    6.0
    """
    rads = math.radians(theta)   # convert degrees into radians
    dx = b * math.cos(rads) - a  # distance between x-values of the points
    dy = b * math.sin(rads)      # distance between y-values of the points
    return (dx ** 2 + dy ** 2) ** 0.5


def total_distance(points: Tuple[float, ...], theta: float = 15) -> float:
    """Return the total distance of alternating points between two lines."""
    # calculate the distances between consecutive points, and sum all segments
    # add a 1.0 to the start of the points tuple because that's where we start
    points = (1.0,) + tuple(points)
    return sum(distance(a, b, theta) for a, b in zip(points, points[1:]))


if __name__ == "__main__":
    # solve for the base case of choosing three points to minimize distance
    result = minimize(total_distance, x0=(1.0, 1.0, 1.0), args=15)
    print(result)

#       fun: 0.7071067811865541
#  hess_inv: array([[0.3980166 , 0.35710939, 0.34512563],
#        [0.35710939, 0.55406504, 0.53529042],
#        [0.34512563, 0.53529042, 0.70655101]])
#       jac: array([ 7.45058060e-08, -4.47034836e-08, -1.49011612e-08])
#   message: 'Optimization terminated successfully.'
#      nfev: 40
#       nit: 7
#      njev: 10
#    status: 0
#   success: True
#         x: array([0.81649653, 0.73205072, 0.70710669])

Riddler Ants

Setup

The Math

Solution

Extending the Problem

Full Code